La página de Reijavo

Aquiles y la tortuga

Alguna vez escuché mencionar la paradoja de Aquiles con la tortuga. Para situarnos un poco en el contexto, Aquiles es un héroe griego quien según la mitología era inmortal, salvo por su talón que constituía su punto débil -de ahí el dicho "el talón de Aquiles" en referencia a los puntos débiles-. Homero nos cuenta en la Ilíada que Aquiles era conocido como "el de los pies ligeros", por su gracia y velocidad al correr.

Tomando a Aquiles como protagonista se formuló la paradoja de Aquiles y la tortuga. Pero antes de hablar de la paradoja expliquemos qué es. Una paradoja es una idea lógica mente correcta, pero que es contradictoria con su misma definición. Existe la categoría llamada "paradojas de Zenón", las cuales fueron formuladas para demostrar que las sensaciones que obtenemos del mundo son ilusorias. Por ejemplo decían que una persona jamás iba a recorrer cierta distancia finita. Actualmente conocemos la unidad metro. Supongamos que una persona quiere recorrer 10 metros. Para hacerlo tendrá que recorrer primero la mitad de eso, es decir 5 metros. Pero para recorrer esos 5 metros debe primero recorrer la mitad de eso. Y para andar esa mitad, debe avanzar la mitad de la mitad y así hasta el infinito, concluyéndose que jamás esa persona podrá moverse del punto inicial. Análogamente se puede demostrar que si quieres pegarle a un árbol con una piedra, jamás saldrá la piedra de tu mano. Porque para recorrer la distancia entre tu mano y el árbol, la piedra tiene que abarcar la mitad primero, pero para abarcar esa mitad, debe recorrer la mitad de esa mitad, y así hasta el infinito en donde la piedra jamás sale de la mano del lanzador.

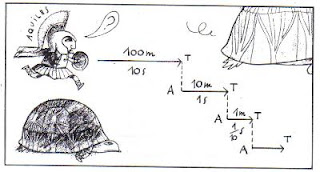
En el caso de Aquiles y la tortuga el caso es el siguiente: Aquiles, el atleta más veloz, capaz de correr los 100 m. en 10 segundos, no podrá alcanzar a una lenta tortuga, diez veces menos rápida que él. Ambos disputan una carrera, concediendo Aquiles una ventaja de 100 m. a la tortuga. Cuando Aquiles ha cubierto esos 100 m., la tortuga se ha desplazado 10 m. Al cubrir Aquiles esos 10 m., la tortuga se ha desplazado 1 m. Mientras cubre ese metro que le separa de la tortuga, ésta ha recorrido 0'1 m. Y así indefinidamente.

Así, Aquiles debe cubrir infinitos trayectos para alcanzar a la tortuga. Por lo tanto, Aquiles deberá cubrir una distancia infinita, para lo cual necesitará un tiempo infinito. De tal manera que el desgraciado Aquiles nunca alcanzará a la tortuga.

Es evidente que esta paradoja, bajo una apariencia de razonamiento correcto, esconde algún fallo... todos sabemos que Aquiles debe alcanzar a la tortuga. Pero se tardó 24 siglos en desvelar por completo, gracias a la Teoría de Límites, cuál era el fallo: la suposición de que infinitos trayectos deben sumar una distancia infinita y necesitan un tiempo infinito no es correcta.

Muchas veces se apela a que las matemáticas son exactas y se aplican a la vida real de forma precisa. Esto es falso y se los voy a demostrar con un ejemplo sencillo. Todos conocen la regla de proporcionalidad inversa, que dice que si una variable aumenta, la otra también disminuye (o viceversa). Ejemplos: "mientras más calor se aplica al agua, más rápido hierve", "mientras menos albañiles trabajen en mi casa, más tiempo se demorarán". Pero acá está al problema, planteemos lo siguiente: Se necesita hacer 1 agujero cuadrado en la tierra,de 1 metro de profundidad. Un hombre se demora un día en hacerlo. Dos hombres, se demorarán medio día, cuatro hombres 6 horas, 8 hombres 3 horas,.....50 hombres media hora?, Piensen!, 50 hombres al mismo tiempo haciendo un hoyo de 1 metro jamás terminarían en media hora porque lo único que harían sería estorbarse!

Es increible cómo existen ejemplos similares en que la lógica matemática pareciera sucumbir ante la temible, compleja y estocástica realidad.